Conifolds and “The (Real Worlds-Wide-)Web”Home | Bio | CV | Courses | Research | Other
Conifolds and “The (Real Worlds-Wide-)Web”| Conifold [5] | n. | A space that is smooth apart from a finite number of isolated crepant singularities —which can be smoothed without changing the canonical (1st Chern) class. |
| adj. | relating to, or involving conifolds. | |
| The Web [D. M.] | The web of all superstring compactifications (on Calabi-Yau 3-folds). |
|
In 1986/87, in my final Ph.D. graduate student year at University of Maryland at College Park, I was working on Ref. [–3] and with Paul S. Green from the Math Department of University of Maryland at College Park on Ref. [–2], and—unbeknownst to each other’s efforts—Philip Candelas et al. were working on Ref. [–1]. We have independently noticed that constructions of Calabi-Yau 3-folds can be turned one into another, and started observing the regularities—some of this made it into Section III of Ref. [–1]. Philip and I met in the summer of 1987 at the ICTP in Trieste, where he showed me the voluminous computer listing, realizing that we were working on the same topic. In the Fall 1987, I joined Philip’s research group, within Steven Weinberg’s Theory Group at the University of Texas at Austin, but also continued collaboration with Paul S. Green.
In 1987, Paul noticed Miles Reid’s article [0], describing a transition consisting of replacing a (homology class of) 2-sphere(s) with a (homology class of) 3-sphere(s) or vice versa, and his two-fold conjecture:
(1) that all Calabi-Yau 3-folds are so connected, and
(2) that this transition is never obstructed, thus giving rise to an indefinite connected web of Calabi-Yau 3-folds.
Paul and I then proved [1,2] Reid’s conjecture within almost all the then known constructions:
are all connected one to another through Reid’s transition. The same is then true of all compactifications of higher-dimensional theories, including but not limited to superstrings. In turn, Reid’s conjecture is correspondingly applicable to all such compactifications, and would imply that there are indefinitely many topological types of superstring theories compactified to effectively 3+1-dimensional spacetime.
The double solids are suitably branched covers of almost Fano 3-folds [1]. Whereas Fano 3-folds have been classified by Mori and Mukai [Man. Math. 36 (1981) 147], and come in 87 topological types, almost Fano 3-folds (with a semi-positive canonical class, such that the anticanonical sheaf has at least one global section) have not been classified, nor is it known if there are any Calabi-Yau double solids from Ref. [1] that are not in the list of 7868 Calabi-Yau complete intersections in products of projective spaces.
Much of 1987/88 was devoted to studying the implications of this connectedness to the geometry of the moduli space. We proved that the conifolds are at finite distance from smooth models [3], in the Weil-Petersson metric that turns out to be equal to Zamolodchikov’s worldsheet field theoretic one [4]. This all becomes part-and-parcel of the special geometry (á la Bryant-Griffiths) description of the space of complex structures of Calabi-Yau 3-folds [5].
Whereas we have initially had in mind only nodes (A1 singularities, in Arnold’s classification), it soon became obvious that the generalization to crepant singularities is both natural and necessary. (Paraphrasing Miles Reid: When a singularity is smoothed, it is replaced by local surgery with an ‘exceptional set’ and this most likely contributes to the canonical class. If it does, there is a discrepancy between the canonical classes before and after smoothing; those singularities the smoothing of which incurs no discrepancy are crepant. Got it? As it has no discrepancy, it is not discrepant, and so is crepant. I guess, crepant sounds better than ‘undiscrepant’.)
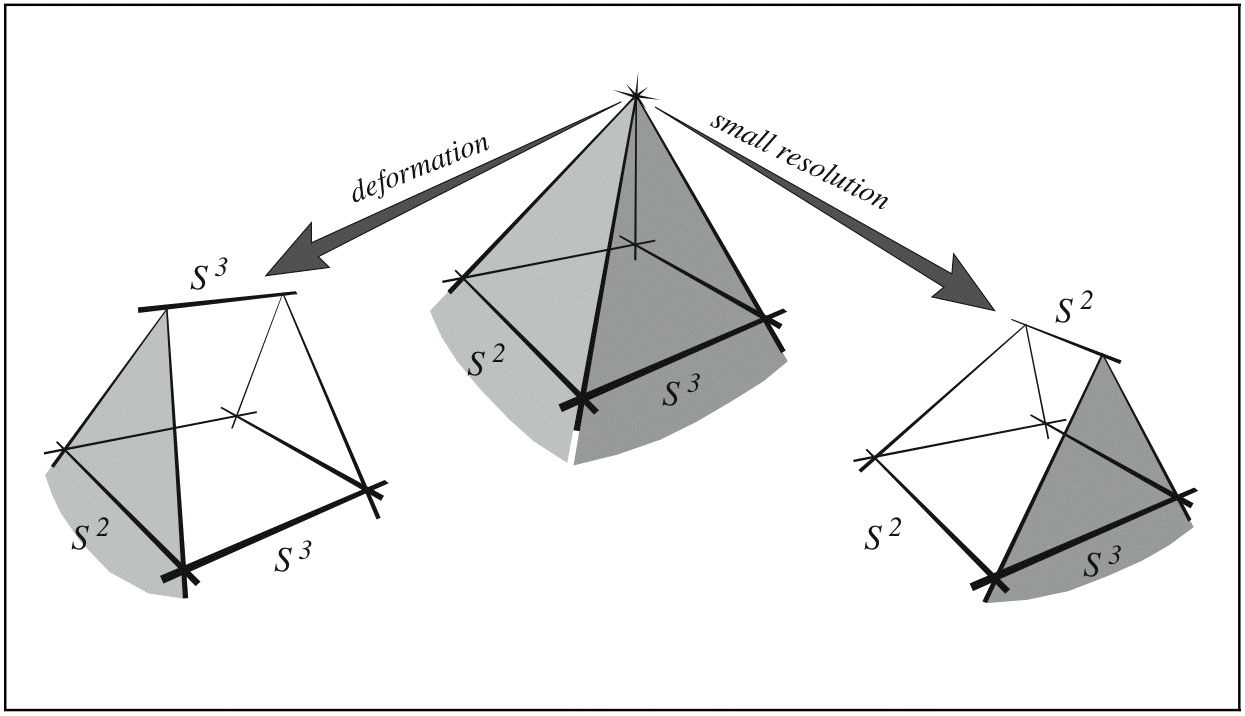
The works [1, 2, 3, 5] all describe the simplest case of Reid’s transition (a.k.a., the conifold, extremal, geometric transition, sometimes understood with some distinctions) whereby the topology type of the Calabi-Yau 3-folds changes—at the conifold, X #. At either ‘side’ of it are smooth Calabi-Yau 3-folds: its smooth deformation, X b, and its small resolution, X r. While X b changes (with the “vanishing S 3-like cycles” shrinking) as it is becoming closer and closer to the singular X #, the topology type of X b remains constant. Then, it abruptly changes to X #, the “vanishing S 3-like cycles” having collapsed the singular nodes. And then it again abruptly changes to X r, the nodes having turned into infinitesimal S 2-like (with compatible complex structure, ℂℙ1-like) “exceptional sets.” As these S 2s grow in sizee, the topology type of X r remains constant. Locally, where the conifold, X #, had a single singular node, its smooth deformation, X b, has a 3-sphere, and its small resolution, X r, has a 2-sphere:
Feel free to use the original grayscale PDF version
of this illustration, and/or its more recent, colored
PDF version.
I devised this diagram for the purposes of Ref. [5], where it was rendered within the limited LaTeX picture environment; this image is from Ref. [6]. Earlier, Ref. [–1] visualized the transition by presenting what looks very much like the 2-dimensional analogue of the transition—and which illustrations in fact do describe the analogous transition whereby a Riemann surface reduces genus by one, owing to a local surgery that replaces a circle (i.e., a 1-sphere) by a singular node and then by a double point—which in fact is a 0-sphere. While this real 2-dimensional analogy captures some of the properties of the complex 3-dimensional transition, it fails to be faithful in other aspects. In particular, the real 2-dimensional “S 1 ↔ S 0” transition changes π1 and for genus-0 also π0, and it also changes the canonical class. The complex 3-dimensional, “S 3 ↔ S 2” transition changes neither of those — and this is faithfully depicted in the above, “tents” diagram. (It does change π3 and π2, of course.) In fact, this depiction of the transition permits a much more detailed analysis; see Chapter D of Ref. [6].
Reid’s “S 3 ↔ S 2” transition necessarily changes the Euler number of the Calabi-Yau 3-folds involved in the transition. This, in turn, equals Witten’s supersymmetry index for the supersymmetric worldsheet theory of the superstrings compactified on the Calabi-Yau 3-fold. Refs. [1, 2, 5] duly cautioned that these are phase transitions and so inherently non-perturbative, and Refs. [7, 8] demonstrate the inadequacy of the known worldsheet conformal field theory approach. The lack of understanding of the physical mechanism that would make Witten’s supersymmetry index change prevented general acceptance of these results at the time.
Attitudes started changing only after Brian Greene, David Morrison and Andrew Strominger showed—in the more restrictive context of Type II theories (and where Witten’s supersymmetry index is a continuous characteristic function, interpolating between the Euler number and the Arithmetic genus, and so is not a definite number, much less an integer)—that the topology change occurs via certain massive black hole-like states turning massless and so providing the requisite additional degrees of freedom corresponding to “vanishing cycles” [9]. (This result was published back-to-back with Strominger’s brand-new analysis of how the black hole-like states turning massless on conifolds correct the conformal field theory analysis [10].) In the heterotic string case, the transition remains not fully understood except for the suggestion that it must involve “nontrivial interacting fixed points’ [11], and even used to study associated Type II string theory transitions in 3-dimensional spacetime [12]. By 2002, Maximilian Kreuzer and Harald Skarke provided a computer-generation of 473,800,776 toric constructions of Calabi-Yau 3-folds, which contain 30,108 distinct Hodge diamonds, but presumably at least an order of magnitude more topological types of Calabi-Yau 3-folds; all of these are connected [13] in a sense defined by Kreuzer and Skarke; this may well equal Reid’s transition, but is far from obvious. Thus, proving—rigorously—that Reid’s “deformation ↔ small resolution” transition indeed suffices to connect all these Calabi-Yau 3-folds remains an open problem: Singularities are also classified (by Arnold and Gusein-Zade) in terms of their severity and number of parameters they admit. Clearly, the simplest are isolated and their small resolution requires a string of S 2’s (connected as in the Dyinkin diagram of an A-D-E Lie algebra) instead of a single S 2; Reid’s basic idea, nevertheless, is the same. Interestingly, conifold transitions can also be used to construct still new Calabi-Yau 3-folds, both simply-connected [14], and multiply-connected [15].
To the best of my knowledge, there do exist sporadic constructions of Calabi-Yau 3-folds—sporadic in the sense that I only know of a few examples and know of no systematic analysis, and sporadic in the sense that I do not know of them being proven to be describable as one of the toric constructions in Ref. [13]. Such an example is the Pfafian variety of which I learned from Sheldon Katz, and which is described in section 3.5 of Ref. [6]. Other families of examples can be constructed as embeddings in generalized flag-varieties; see Sections 3.3, 3.5 and 9.5 in Ref. [6]. In addition, there are also minimal blow-ups of global finite quotients of 6-tori, T 6/G, where G is a discrete symmetry group of the 6-torus, T 6. I do not know of any systematic and comprehensive study that extends the proof of Reid’s conjecture to all known constructions of Calabi-Yau 3-fold, nor do I know of any intrinsic proof, that does not rely on the construction of a class of Calabi-Yau 3-folds. So, both aspects of Reid’s conjecture remain open:
(1) connectivity of all Calabi-Yau 3-folds, and
(2) indefinite applicability of Reid’s transition to generate an indefinitely large universal Calabi-Yau 3-fold.
Note the curious 7-year rhythm: 1988: [1, 2] — 1995: [9, 10] — 2002: [13]… and 2009: …
Well, late 2009 and early 2011 seem to have brought finite quotient conical (“hyperconifold”) singularities in the fold, and thereby the possibility to connect multiply connected Calabi-Yau spaces with the simply connected ones [16, 17], the latter of which showing that “hyperconifold” transitions can be mirrors of “ordinary conifold transitions” (funny how “preposterous” and “nonsense” turns into “ordinary” :-).
And then, eleven years later, the story continues with a much more (’brane-)complete analysis of the conifold transition for heterotic strings [18] …
Calabi-Yau sites
Calabi-Yau Data (Maximilian Kreuzer)
Calabi-Yau Home Page
(Rolf Schimmrigk & Andreas Wißkirchen)
©2022, Tristan Hübsch