Home |
Bio |
CV |
Courses |
Research |
Other
 BOOK:
BOOK:
- Calabi-Yau Manifolds
— A Bestiary for Physicists
- (World
Scientific, Singapore, 1992; hardcover)
- + 2nd, corrected and expanded edition
- (World Scientific, Singapore, 1994; paperback)
[ A ]
[ B ]
[ WSci, DOI:10.1142/1410 ]
- for reviews, see: Physics Today, 6/93, p. 93-94 (by E. Witten),
and Zentralblatt für Mathematik 771 (1993) 53002 (by J.D. Zund) [Zbl 0771.53002].
Cover photograph by Donna D'Fini.
- ERRATA (2nd, paperback edition from 1994):
- “p.n” = page n;
“P.n” = paragraph n;
“l.n” = line n, n > 0 is counted downward , n < 0 upward;
“S.m.n” = section n of chapter m.
If you notice any kind of error in the book, please, do let me know!
- p. 15, l.–2, (end of S.0.4): “ understood n” → “ understood modulo n ”.
- p. 32, Eq. (1.2.15): the right-hand side should have an overall minus. That is, χE = 2(b1,1 – b2,1)
- p. 37, Eq. (1.3.19): the middle term should be “ = c(Σi ℒi) = Πi
c(ℒi) = ”. [Philippe Spindel, thanks!]
- p. 39, Eq. (1.3.27): the “ 1/n! ” normalization of the integral is a convention, alas different from that in Eq. (1.3.28) and later:
- The equality Eq. (1.3.27) is in agreement with Wirtinger’s theorem and inequality; see, e.g., the Wikipedia entry, p.31 or Principles of Algebraic Geometry by P. Griffiths and J. Harris (John Wiley & Sons, 1978) or S.3.1, p.136 of Intrduction to Complex Analysis by E.M. Chirka, P. Dolbeault, G.M. Khenkin and A.G. Vitushkin (Springer, 1997).
However, it is standard to omit the “ 1/n! ” normalization factor in intersection computations, which re-normalizes the relation between the 2n-volume of a hypersurface and its Euler number as given in Eq. (1.3.28). [Philippe Spindel, thanks!]
- p. 42, Eqs. (1.5.5) and (1.5.6): the last terms miss a prime; “ ... ch[V ]” → “ ... ch[V' ] ”
- p. 43, Eq. (1.5.10): the last term misses a prime; “ ... ∧ td[V ]” → “ ... ∧ td[V' ] ”
- p. 44, Eqs. (1.6.1), (1.6.2) and p. 336, Eq. (L.40): The left- and right-hand sides of the j-map should be swapped for the j-maps to be onto/surjective as stated. The corresponding (reverse-oriented) maps in co homology are then into/injective. [Nick Warner, thanks!]
- p. 50, Eq. (2.1.16): “ r +1 ” → “ r =1 ” in the lower limit of the 1st summation. [Philippe Spindel, thanks!]
- p. 58, S.2.2.1 l.–1: “ ...space if... ” → “ ...space of... ” .
- p. 71, l.1 below Eq. (2.5.2): “ ...arithmetic genus... ” → “ ...Todd genus... ”.
- The arithmetic genus is pa =
(–1)n(χh–1)
- p. 83, footnote: The Kodaira-Nakano theorem is not applicable as needed. [Karol Palka, thanks!]
- The Kodaira-Nakano theorem guarantees (3.2.1) for Fano 3-folds, but not for almost-Fano 3-folds that are not also Fano, the anti-canonical bundle of which is almost ample not ample. Just how I indended to remedy this in 1990–91 and whether I did have a complete remedy, I cannot remember. However, Palka observes that the defining requirement (introductory sentence of section 3.2.1 [see the article with Paul Green]) is that “ | −KF | is without base points ”, which if amended by [K]3 ≠ 0 is stronger than Miles Reid’s definition of weak Fano, for the latter of which already the vanishing theorem by Kawamata & Vieweg does guarantee (3.2.1). [Karol Palka, thanks!] ... however, the “simple example” (3.2.25) on p. 91 has C13 = 0, — yet explicit calculation (following Chapters 9 and A) verifies the Hodge diamond as given in (3.2.1). Might the assumed basepoint-freedom of the anticanonical line-bundle imply (3.2.1) all by itself?
- p. 86, l.1: the relative sign in the definition of genus is negative: “ 1 + ½ C1n ” → “1 − ½ C1n”, as well as “1 + ½ χE” → “ 1 − ½ χE”.
- p. 87, Table 3.1, last entry: “ [6||2 2 3] ” → “ [6||2 2 2] ”.
- p. 94, P.2, l.4: “ consists some negative ” → “ consists of some negative ”.
- p. 127, Paragraph after Lemma 5.1 (Delorme): The dimensions of the first six (weighted) projective spaces in this paragraph are one less than indicated. Thus:
- “ P3(1:2:2) ≈ P3 ” → “ P2(1:2:2) ≈ P2 ”, “ P4(1:2:4:4) ≈ P4(1:1:2:2) ” → “ P3(1:2:4:4) ≈ P3(1:1:2:2) ” and
“ P5(2:3:6:12:18) ≈ P5(1:1:1:2:3) ” → “ P4(2:3:6:12:18) ≈ P4(1:1:1:2:3) ”.
- p. 131, P.1, last line: “ only at (0:0:0:0:1) and (0:1:0:0:0). ” → “only at (0:0:0:0:1). ”.
- p. 140, Eq. (5.5.1): “ z2 ” → “z2 ”.
- p. 163, P.3, l.1: “ takes incorporates” → “ incorporates⟩ “.
- p. 174, Eq. (8.1.8), penultimate row (first row for d7): “ ±2⟨a,c,c,d⟩” → “ ±2⟨a,d,d,d⟩ “. [Andreas Schachner, thanks!]
- p. 174, Eq. (8.1.9), exponent: “ 2(b1,1+1)” → “ (b1,1+1) “. [Vishnu Jejjala, thanks!]
- p. 178, l.2 after Eq. (8.3.4): “ 2636 ” → “ 2232 “.
- p. 179, l.2 after Eq. (8.3.8): “ 2234132 ” → “ 22132 “.
- p. 184, P.–1, l.–1: “ 40th powers ” → “ 20th powers “.
- p. 210: display (A.1.6) should be
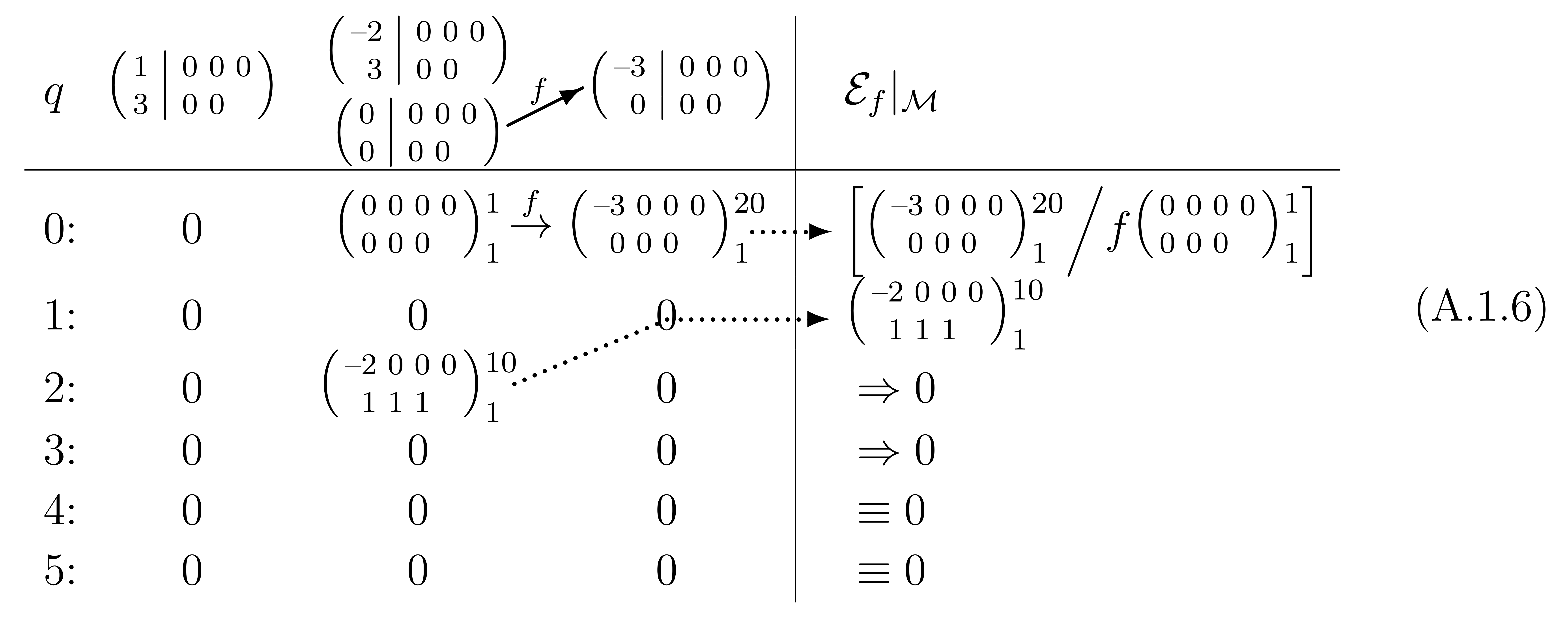
- p. 211: display (A.1.10) should be

- p. 278, P.2, l.1: “ ℳ♯ ” → “ 𝔐♯ ”
- p. 319, in the Lexicon definition of Analytic: “ an(z − z0) ” → “ an(z − z0)n”
- p. 329, l.1 below Eq. (L.21):
“ ...arithmetic genus,...
” → “ ...Todd genus,... ”
- Also, “ ...(number).
” → “ ...(number), while pa is the arithmetic genus. ”
- p. 333, Eq.(L.30): “ 𝕄m×... ” → “ 𝕄n×... ”.
- p. 335, l.5: “ ∧(p–n) ” → “ ∧p–n ”.
- p. 349, title of Ref. [37]: “ Threefolds : and Introduction ” → “ Threefolds: an Introduction ”.
©2024, Tristan Hübsch
 BOOK:
BOOK:
 BOOK:
BOOK:

