Howard University
Washington
DC, 20059
Introduction to
Math. Physics/Math. Methods in Physics
PHYS-192 (87872) & PHYS-216 (80269): MW: 8:40–10:00
am, Thirkield Hall, Rm. 103
[Topics] [Daily
Schedule] [Minimal Requirements] [Assignments] →
[eGear1] [eGear2]
- Instructor: Tristan Hübsch
- Office hours: MT 2:30–5:00 pm, W 2:30–3:45 pm, and by appointment (a day in advance); check my weekly schedule
Office: Thirkield Hall #213, 202-806-6267,
thubsch@mac.com or
thubsch@howard.edu
- Textbook (required): G.B.
Arfken, H.J. Weber and F.E. Harris, Mathematical
Methods for Physicists (7th
ed.)
- (optional) F.W.
Byron & R.W. Fuller, Mathematics of Classical and
Quantum Physics
- (optional) J.
Mathews & R.L. Walker, Mathematical Methods of
Physics
- (optional) K.F.
Riley, M.P. Hobson & S.J. Bence, Mathematical Methods
for Physics and Engineering
- (optional) K.
Cahill, Physical Mathematics
- (optional) M.
Vaughn, Introduction to Mathematical
Physics
- (optional) S.
Hassani, Mathematical Physics A Modern Introduction to Its
Foundations
- This is a service course: its material serves to
support other courses in the curriculum. The literature provided
here, together with all additional materials distributed during
the course, must therefore be regarded as supporting resources.
Grading recipe (no make-ups are offered, except in cases of
documented medical or family emergency):
| Component |
Time |
Remark |
% of Grade |
| Homework |
See in daily schedule |
Late HW = 0 credit !!! |
20% |
| Classwork/Quizzes |
≤ 2/week, unannounced |
current material; short and straightforward |
20% |
Midterm Exams
(two) |
See in daily schedule |
material covered since the previous exam |
20% (each) |
| Drop the one worst of the above
components (for each student individually). |
| Final exam |
Last week of semester |
comprehensive: complete course content |
40% |
— See also the minimal requirements for passing
the course —
This course presents a review and practice of: (1) basic vector and tensor analysis, (2) ordinary and partial differential equations, (3) linear algebra and linear systems of algebraic and differential equarions (including eigenvalues & eigenvectors), (4) infinite series and products, and (5) complex analysis (including residues). The focus is more on applications of the listed material than on proofs of the results, while maintaining mathematical rigor. Ultimately, this is a prerequisite and an adequate preparation for the 2nd half of the course, which focuses on (1) general Sturm-Liouville theory (and all the “special functions”), (2) group theory, (3) integral transforms and Hilbert-Smidt theory, (4) calculus of variations and (5) probability and statistics.
“Success = 1% inspiration + 99%
perspiration” —T.A. Edison
However, learning is still 100% learning!
Topical Schedule
|
| §1–2 |
|
Preliminary Reminders, Matrices and
Determinants |
| §3 |
|
Vector Analysis in Flat Space |
| §7 |
|
Ordinary Differential Equations |
| 1st Midterm exam,
§1–3 & 7:
Wednesday, 09/24
open-text, in-class & take-home
due Monday, 09/29 |
| §19 |
|
Fourier Series: Analysis and Synthesis |
| §9–10 |
|
Partial Differential Equations and Green’s Functions |
| §14–16 |
|
Bessel, Legendre and Trigonometric (BLT) Equations and the
Angular Momentum Algebra |
| 2nd Midterm exam,
§9–10, 14–16 & 19:
Wednesday, 10/29
open-text, in-class & take-home
due Monday, 11/03 |
| §11 |
|
Complex Analysis |
| §6 |
|
Linear Systems, Eigenvalues and Eigenvectors (Linear
Algebra) |
| §4 |
|
Tensors in General Coordinates, Differential Forms and
Integral Characteristics |
Final exam,
comprehensive: given
Wednesday, 11/19 — due Monday, 12/01
|
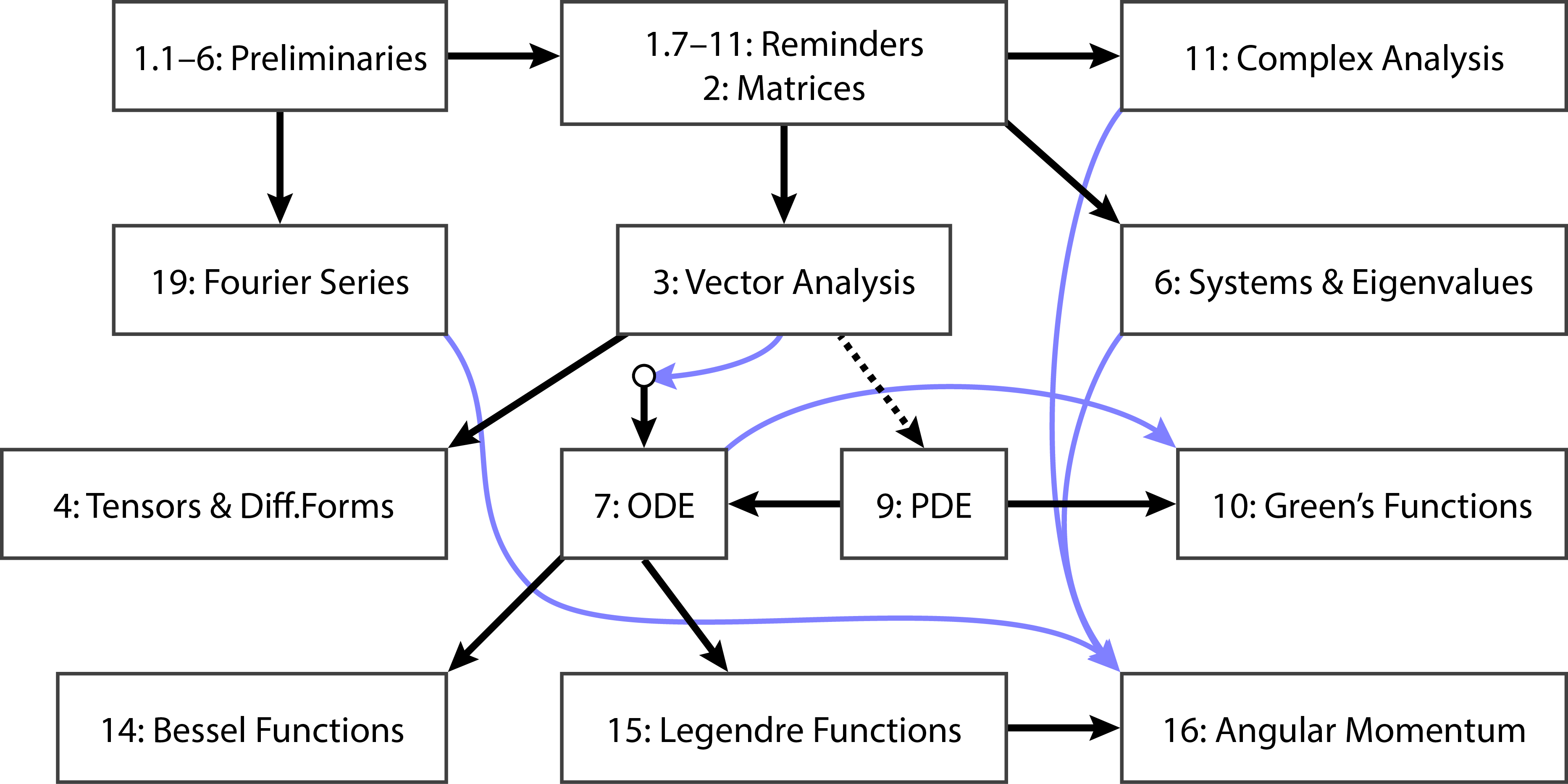
| The pre-requisite and co-dependence chart of
the material covered in this course: |
 |
Day-to-Day Schedule
|
| —
Students are required to read ahead and prepare for class —
|
| 08/18 |
|
D.01
|
Introduction and Preliminary Reminders: §1.1–3 |
| 08/20 |
|
D.02
|
Preliminary Reminders: §1.4–6 |
| 08/25 |
|
D.03
|
Preliminary Reminders: §1.8–11 |
| 08/27 |
|
D.04
|
Vectors, Matrices and Linear Algebra: §1.7 & §2 [HW1 due] |
| 09/01 |
|
Observed Holiday:
Labor Day |
| 09/03 |
|
D.05
|
3D Vector Algebra: §3.1–4 [HW2 due] |
| 09/08 |
|
D.06
|
3D Vector Calculus (Derivatives): §3.5–6, Derivatives |
| 09/10 |
|
D.07
|
3D Vector Calculus (Integrals): §3.7–9 +more
[HW3 due] |
| 09/15 |
|
D.08
|
Curvilinear Coordinates: §3.10;
Ordinary Differential Equations: §7.1–3 |
| 09/17 |
|
D.09
|
Ordinary Differential Equations: §7.4–5 [HW4 due] |
| 09/22 |
|
D.10
|
Inhomogeneous and Nonlinear Differential Equations: §7.6–8 |
| 09/24 |
|
—
|
1st Midterm Exam (§1, 2, 3 & 7), open-text;
in-class part due by end of class
& take-home part
due Monday, 09/29, 12:00 am (midnight, end of day) |
| 09/29 |
|
D.11
|
Fourier Series: §19 +more;
1st Midterm Exam due by 12:00 am (midnight, end of day) |
| 10/01 |
|
D.12
|
Partial Differential Equations: §9.1–4 [HW5 due] |
| 10/06 |
|
D.13
|
Partial Differential Equations: §9.5–8;
Green’s Functions: §10 |
| 10/08 |
|
D.14
|
Bessel Functions, Generating Function, Orthogonality: §14.1–4
[HW6 due] |
| 10/13 |
|
University closed:
Mental Health Day |
| 10/15 |
|
D.15
|
Modified Bessel Functions & Various Dimensions: §14.5–7 [HW7 due] |
| 10/20 |
|
D.16
|
Legendre Polynomials, Cousins & Spherical Harmonics: §15 |
| 10/22 |
|
D.17
|
Angular Momentum Operator Algebra: §16.1 [HW8 due] |
| 10/27 |
|
D.18
|
Angular Momentum Operator Algebra: §16.2–4 |
| 10/29 |
|
—
|
→ 2nd Midterm Exam
(§9, 10, 14–16 & 19), open-text;
in-class part due by end of class
& take-home part
due Monday, 11/03, 12:00 am (midnight, end of day) |
| 11/03 |
|
D.19a
|
Complex Analysis: Derivatives, Integrals & Cauchy’s Theorem & Formula §11.1–4;
2nd Midterm Exam due by 12:00 am (midnight, end of day) |
| 11/05 |
|
D.19b |
Complex Analysis: Laurent Expansion & Singularities §11.5–6 [HW9 due] |
| 11/10 |
|
D.20 |
Complex Analysis: Calculus of Residues §11.7 |
| 11/12 |
|
D.21
|
Complex Analysis: Computing Integrals §11.8–10 [HW10 due] |
| 11/17 |
|
D.22
|
Hermitian Matrices, Eigenvalues & Eigenvectors:
§6.3–4 |
| 11/19 |
|
D.23
|
Normal Matrices, etc. §6.5 +more [HW11 due]
→ Final Exam given;
due Monday, 12/01, 12:00 am (midnight, end of day) |
| 11/24 |
|
D.24
|
Tensor Analysis & Calculus: §4.1–4 |
| 11/26 |
|
D.25
|
Tensor Analysis, Differential Forms & Integral Characteristics: §4.5–7 [HW12 due] |
| 11/27 – 11/30:
Observed Holiday: Thanksgivings |
| 12/01 |
|
→
Final Exam due by 12:00 am (midnight, end of day) |
| All indicated times and deadlines cite “Eastern time,” standard or daylight-saving — as officially adopted by Howard University.
|
Minimal Requirements
To pass the course with a grade B or better, a graduate Student
must by the time of the final exam be able to demonstrate the
ability to:
- perform vector and simple tensor calculus, as
typically needed in physics problems;
- solve rectangular, cylindrical and spherical
boundary-valued problems;
- expand real functions into Taylor series and
calculate with such series;
- expand complex functions into Laurent series and
evaluate integrals using residues;
- determine the eigenvalues and eigenvectors of a
2×2 and 3×3 square matrix.
A graduate student who cannot demonstrate the above-listed skills
by the time of the final exam automatically forfeits a grade of B
or better — regardless of the total number of points acquired in
homework, quizzes and exams.
Homework assignments (60 Shades
of Hard)
|
| # |
Due |
Problems |
| 1. |
08/27: |
1.1.6 [p.11], 1.1.11.a [p.13], 1.2.1 [p.24],
1.2.8 [32], 1.3.7 [p.37] |
| 2. |
09/03: |
1.7.7 [p.53], 1.8.6 [p.61], 1.10.1 (only the 1st-line statement!) [p.74], 2.1.1 [p.93], 2.2.7 [p.115]
(see Table 1.2, p.66; the “2nd line of 1.10.1” pertains to Ex.1.10.2–1.10.9) |
| 3. |
09/10: |
3.2.10 [p.132], 3.3.2 [p.138], 3.5.9 [p.153],
3.6.5 [p.157], 3.6.9 [p.158] |
| 4. |
09/17: |
3.7.2 [p.163], 3.8.8 & 3.8.10[p.170], 3.9.1
[p.180], 3.10.16 [p.199] |
| 5. |
10/01: |
7.2.13 [p.341], 7.4.1 [p.346], 7.5.7 [p.356],
7.6.19 [p.373], 7.8.4 [p.379] |
| 6. |
10/08: |
19.1.5 [p.946], 19.1.13 [p.948], 19.2.6 [p.953],
19.2.13 [p.954], 19.2.19 [p.956] |
| 7. |
10/15: |
9.3.1 [p.414], 9.4.2 [p.432], 9.5.1 [p.434],
9.6.3 [p.437], 9.7.3 [p.444] |
| 8. |
10/22: |
10.1.4 [p.457], 10.2.4 [p.466], 14.2.6 [p.666],
14.5.5 [p.686], 14.7.15 [p.712] |
| 9. |
11/05: |
15.1.5 [p.722], 15.2.12 [p.732], 15.3.3 [p.740],
15.4.3 [p.753], 15.5.7 [p.766] |
| 10. |
11/12: |
16.1.4 [p.783], 16.1.8 [p.784], 16.2.3 &
16.2.5 [p.795], 16.3.4 [p.806] |
| 11. |
11/19: |
11.2.12 [p.477], 11.3.7 [p.485], 11.4.7 [p.492],
11.6.5 [p.507], 11.8.18 [p.541] |
| 12. |
11/26: |
6.2.1 [p.308], 6.2.8 [p.309], 6.4.5 [p.318],
6.5.1 [p.324], 6.5.13 [p.326] |
All written assignments (HW & tests) are due by 12:00 am (midnight), end of the day indicated and should be sent by e-mail as single (bundled) PDF files; to this end, using a camera-to-PDF-scanner app on a smart-phone or tablet is highly recommended. Late homework will not be accepted, except in cases of documented emergency.
Other Matters
Collaboration Policy
Collaboration — but not blind copying — on the homework assignments is strongly encouraged; students should use this to learn from each other. There is no substitute for the diverse previous experiences and wealth of knowledge brought together by a cohort of students. All exams and quizzes are open text and open class-notes (including notebooks and class handouts), but no collaboration is allowed; by signing and submitting the exams and quizzes, the student vouches to have abided by this policy. Violation of this policy is covered under University regulations on academic dishonesty and cheating.
Presentation and Organization
First and foremost: your assignments are your communication to the instructor of the level of expertise to which you have mastered the subject matter covered in the course.
So, while a neat presentation of home,- quiz- and exam-work is not required for full credit, it certainly makes it easier to assess the quality of the work and give the proper credit due. In all cases, include a simple sketch if it might help conveying the approach or the calculations. Where necessary, include all units and symbols such as the measure of an integral, arrow on a vector, vertical bars for the absolute value of a quantity, for the magnitude of a vector or for the determinant of a matrix, etc.
- Homework: Submitted answer sheets should be bundled. The Student’s full name (and ID number) should be indicated on the first (cover) page. Solutions should be labeled and ordered consecutively by the problem numbers. Include all calculation/work and give full reference to any result quoted from any source other than the text, and page/equation number for results quoted from the text. Homework assignments will be graded by a grader with whom unsatisfactory credit should be disputed prior to appealing to the instructor; the instructor may override the grader’s assessment.
- Quizzes: The Student’s full name (and ID number) should be indicated on the first (cover) page, unless otherwise requested at the time of the quiz. Include all calculation/work and give the page/equation number for results quoted from the text. Speed and efficiency is important, but the presentation must be legible.
- Mid-term exams: All exam questions are given on a question sheet and include the detailed point distribution and the place to write in the Student’s full name and ID number. This question sheet is to be affixed on the top of the answer sheets; it will be used to indicate the acquired points, part by part and in total, the average score and the standard deviation. A second copy of the question sheet is to be used for the take-home part in the same manner. The formula by which the points will be summed between the two parts will be given on the question sheet.
- Final exam: All exam questions are given on a question sheet and include the detailed point distribution and the place to write in the Student’s full name and ID number. This question sheet is to be affixed on the top of the answer sheets, in the top-left corner. It will be used to indicate the acquired points, part by part and in total, the average score and the standard deviation. The final exams are stored by the instructor, but are available to the individual student for review after the exam.
★★★ Each assignment is to be submitted (and is date-stamped) by e-mail (→ thubsch@mac.com), as a single PDF file. Handwritten and other “hard-copy” answer-sheets should be scanned and bundled into a single PDF file — there are many smartphone and tablet apps that do this automagically; some printers also include a flatbed scanner, if you prefer.
University Attendance Policy
Class Attendance Restricted to Registered Students: Only students whose names appear on the official course roster are permitted to attend class meetings. Students who are not registered are not permitted to attend or participate in course activities, do not have access to Blackboard, cannot submit course assignments, and will not receive a grade for this course. It is the students’ responsibility to ensure that they are properly registered by the published registration deadline. Requests to add courses after the deadline will not be considered.
ADA Procedures
Howard University is committed to creating an accessible, inclusive, and safe learning environment for all students and providing equal access to students with documented disabilities. Students seeking reasonable accommodation must first register with the Office of Student Services (OSS). There you can engage in a confidential conversation about the process for requesting reasonable accommodations in the classroom and clinical settings, which the Office of Student Services (OSS) determines. Accommodations must be requested each semester. Accommodations are not provided retroactively. If you want to request accommodations, please contact OSS via email at oss.disabilityservices@howard.edu or visit https://howard.edu/disability-services
Statement on Sex and Gender-Based Discrimination, Harassment and Violence
Howard University’s Policy Prohibiting Sex and Gender-Based Discrimination, Sexual Misconduct and Retaliation (aka, the Title IX Policy) prohibits discrimination, harassment, and violence based on sex, gender, gender expression, gender identity, sexual orientation, pregnancy, or marital status. With the exception of certain employees designated as confidential, note that all Howard University employees – including all faculty members – are required to report any information they receive regarding known or suspected prohibited conduct under the Title IX Policy to the Title IX Office (TitleIX@howard.edu or 202-806-2550), regardless of how they learn of it. For confidential support and assistance, you may contact the Interpersonal Violence Prevention Program (202-836-1401) or the University Counseling Service (202-806-7540). To learn more about your rights, resources, and options for reporting and/or seeking confidential support services (including additional confidential resources, both on and off campus), visit titleix.howard.edu.
©2025,
Tristan Hübsch
