DEPARTMENT OF PHYSICS AND ASTRONOMY -- (202) 806-6245 (main office), -5830 (fax)
Fundamental Particle Physics 1 (PHYS-228-01, CRN: 89994) M 3:40 – 6:10 pm;
Office hrs.: (MW 10:00 am–12:00 noon, T: 2:00–4:00 pm & by appointment)
[Topics][Daily Schedule][Minimal Requirements][Assignments][e-Gear][Welcome]
|
Component
|
Due time
|
Remark
|
% Grade
|
|---|---|---|---|
| Homework | See in daily schedule | Late HW = 0 credit !!! |
70%
|
| Term project and presentation | End of class | 25 min. + 10 min. questions |
30%
|
The aim of the course is to give a brief but uncompromising introduction to the contemporary theoretical description of the fundamental physics of elementary particles and fields. A review of the scientific methodology, practical aspects such as dimensional analysis, and the field during the XX century introduces the concepts and ideas in their historical perspective, and is followed by an introduction to Lorentz-covariant Feynman calculus. This leads to the Quark Model and the gauge theory (abelian and non-abelian) foundation of Yang-Mills theories of electromagnetic and strong interactions, including an introduction to renormalization and quantum anomalies.
The second part of this course will cover and introduction to the Standard Model, Grand-Unified Theories, general relativity and geometrization of physics, supersymmetry and (super)strings, ushering the Student into the fundamental physics of the III millennium.
“Success = 1% inspiration + 99% perspiration”--T.A. Edison
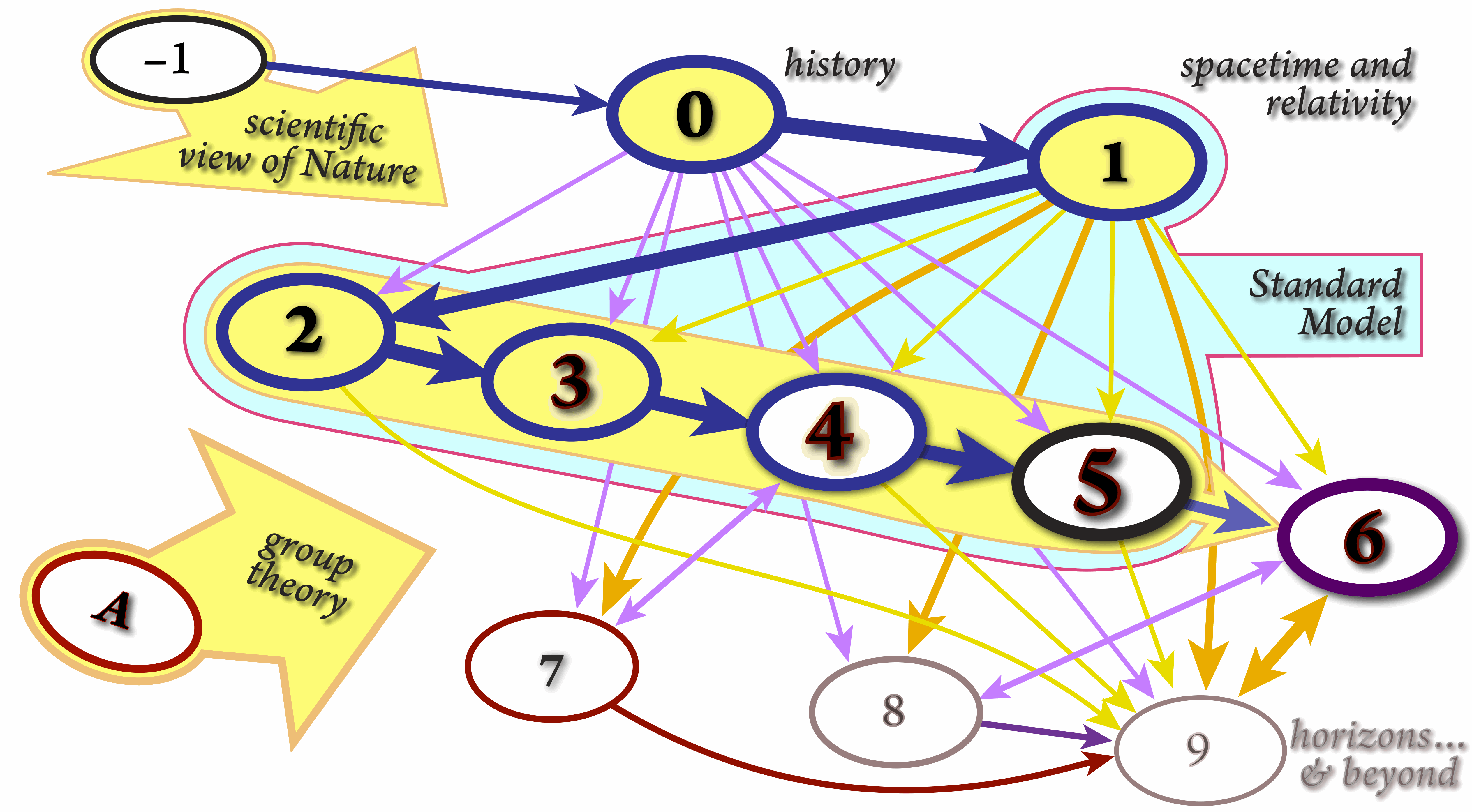
–1. |
The Nature of Observing Nature |
|---|---|
0. |
Fundamental Physics: Elementary Particles and Processes |
1. |
Physics in Spacetime |
2. |
The Quark Model: Combinatorics and Groups |
3. |
Gauge Symmetries and Interactions |
4. |
Nonabelian Gauge Symmetries and Interactions |

| W. of | Ch. |
Topics to be Covered |
|---|---|---|
| 08/22 | –1. |
Fundamental physics; Dimensional analysis; Quantum-relativistic limits of observation; |
0. |
Production, detection and experiments; a historical inventory of particle physics; Conservation laws and rules; |
|
| 09/05 | 1.1 |
Space-time and energy-momentum mixing, Lorentz transformations, tensors and tensor calculus in flat spacetime; |
| 09/12 | 1.2 |
Relativistic kinematics; Two- and more-particle decays; Elastic and inelastic scattering and process threshold; |
| 09/19 | 1.3 |
Diagrammatic representation of pertubation theory; Feynman diagrams and perturbative computation of amplitudes; |
| 09/26 | 2.1 |
Bound states: non-relativistic hydrogen atom and its various corrections as a paradigm; positronium as its counter-point; |
| 10/03 | 2.2–4 |
Finite symmetries & CPT-theorem; Isospin and SU(2); Eightfold way and SU(3)f ; SU(3)c; Hadron masses and magnetic momenta; |
| 10/10 | 3.1–2 |
The gauge principle and a nonrelativistic U(1) example; Dirac fermions; Relativistic electrodynamics of leptons; |
| 10/17 | 3.3 |
QED: quantum electrodynamics of leptons: Feynman rules, lepton-(anti)lepton scattering; Renormalization; |
| 10/24 | 3.4 |
Quantum electrodynamics of leptons and hadrons; Experimental proof of the parton model; |
| 10/31 | 4.1 |
Non-abelian gauge symmetry; Lagrangian density of chromodynamics, color-conservation law and equations of motion; |
| 11/07 | 4.2 |
QCD: quantum chromodynamics: Feynman rules; Quark-(anti)quark interaction & color antisymmetrization; |
| 11/14 | 4.2 |
Renormalization, color confinement, anti-screening and asymptotic freedom; Running coupling parameters; |
| 11/21 | Student presentations |
|
| 11/28 | 4.3 |
Nonperturbative comments: strong CP-violation, Weinberg-Witten theorem, anomalies and anomaly cancellation. |
An invited lecture to a general audience, Discovering the Nucleus of the Indivisible, presented at University of Central Florida, on 29th of September, 2011.
Homework assignments will consist of (1) working out the worked examples end-of-section problems and (2) proof-reading, fact-checking and correcting the developing text, as it is delivered in the classes.
Collaboration policy
One of the aims of this course is to foster collaborative team-work on the subject. The final presentation is however expected to be individual work of each Student and is supposed to showcase the Student’s mastery of the subject.
ADA disclaimer
Howard University is committed to providing an educational environment that
is accessible to all students. In accordance with this policy [details], students
in need of accommodations due to a disability should contact the Office of the Dean for Special Student Services at 202-238-2420, for
verification and determination of reasonable accommodations as soon as possible
after admission to the Law School, or at the beginning of each semester.
© Tristan Hübsch, 2011